Feature Recognition in Scientific Data


Project Description

Currently, the rate at which simulation data can be generated far outstrips the rate at which scientists can inspect and analyze it. 3D visualization techniques provide a partial solution to this problem, allowing an expert to scan large data sets, identifying and classifying important features and zeroing in on areas that require a closer look. Proficiency in this type of analysis, however, requires significant training in a variety of disciplines.
An expert analyst must be familiar with domain science, numerical simulation, visualization methods, data formats, and the details of how to move data across heterogeneous computation and memory networks, among other things. At the same time, the sheer volume of these data sets makes this task not only arduous, but also highly repetitive. One logical next step is to automate the feature recognition and characterization process so scientists can spend their time analyzing the science behind promising or unusual regions in their data, rather than wading through the mechanistic details of the data analysis. The goal of this project was to develop a tool that does so.

General definitions of features are remarkably hard to phrase; most of those in the literature fall back upon ill-defined words like unusual or interesting or coherent. Features are often far easier to recognize than to describe, and they are also highly domain-dependent. The structures on which an expert analyst chooses to focus — as well as the manner in which he or she reasons about them — necessarily depend upon the physics that is involved, as well as upon the nature of the investigation. Meteorologists and oceanographers are interested in storms and gyres, while astrophysicists search for galaxies and pulsars, and molecular biologists classify parts of molecules as alpha-helices and beta-sheets. Data types vary — pressure, temperature, velocity, vorticity, etc. — and a critical part of the analyst’s expert knowledge is knowing how different features manifest in different data fields.

Our goal was to create a general-purpose feature characterization system and to validate it with a variety of specific instances of problems in different fields. As a first step, we focus on finite element analysis data from computer simulations of solid mechanics problems. Since we want to produce a practical, useful tool, we are working with data from deployed simulators, in a real-world format: ASCI’s DMF (Data Models & Formats), a lingua franca used by several of the US national labs to read and write data files for large simulation projects.
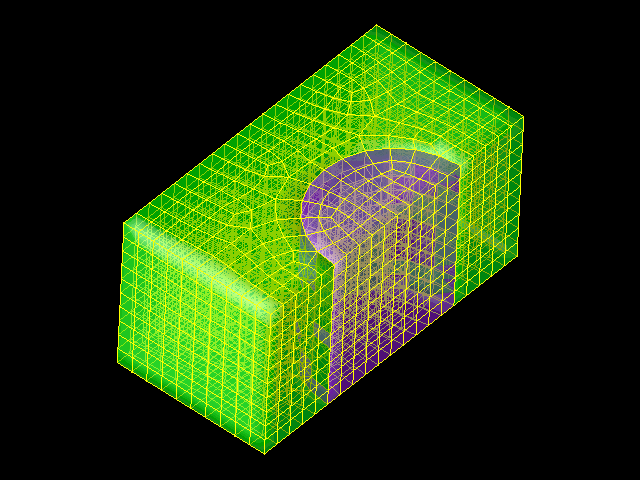
This choice raised some interesting interoperability issues that are described in the papers cited below. A DMF data snapshot consists of a geometric description of a mesh (generally 2D or 3D) and some information about the physics at each mesh point.
Here is an example of such a snapshot– a simple meshed surface in 3D:

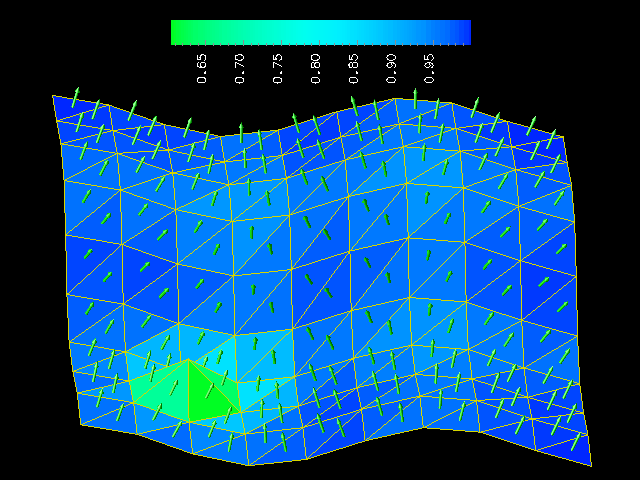
Given such a snapshot, our goal is to characterize the features therein and generate a meaningful report. In this case, the surface is basically smooth with the exception of a single “spike.” Spikes are interesting for both numerical and physical reasons, and our algorithms use patterns in the normals to adjacent mesh elements in order to find them. The image below shows the same surface, but with each mesh element rendered in a color that indicates how much its normal vector deviates from the average of the normal vectors of its neighbors:

In order to understand what makes a feature, we began by working closely with domain scientists to identify a simple ontology of distinctive coherent structures that help them understand and evaluate the dynamics of the problem at hand. (Formally, an ontology seeks to distill the most basic concepts of a system down into a set of well defined nouns and verbs – objects and operators – that support effective reasoning about the system.) In finite-element applications, as in many others, there are two kinds of features that are of particular interest to us:

  • those that violate the continuity and smoothness assumptions that are inherent in both the laws of physics and of numerical simulation: spikes, cracks, tears, wrinkles, etc. --- either in the mesh geometry or in the physics variables.
  • those that violate higher-level physical laws, such as the requirement for normal forces to be equal and opposite when two surfaces meet (such violations are referred to as ``contact problems'').

Note that we are assuming that expert users can describe these features mathematically; many approaches to automated feature detection do not make this assumption. The knowledge engineering process and the algorithms that we use to encapsulate the resulting characterizations, which rely on fairly basic mathematics, are described in the papers cited below, as are the test results.

People

Papers

Support

  • The DOE ASCI program through a Level 3 grant from Sandia National Laboratories
  • a Packard Fellowship in Science and Engineering.
  • Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of these organizations.